Geometry¶
Basic construction elements are simple geometry types, that are used for shape definition of structural members and geometrical object. With defining the further attributes to these elements from the lists Structural analysis elements, Supports and hinges and Loads the complete structural model is created. All values refer to the list StrucutralPointConnection.
Geometry types¶
Geometry type |
Type definition |
Insertion data explanation |
SAF geometry strings |
Notes |
|
|---|---|---|---|---|---|
|
Line |
Straight-line between two nodes |
Start point , End point N1;N2 |
Line |
- |
|
Circular Arc |
Arch defined with 3 nodes |
Start point, Intermediate point, End point N3;N4;N5 |
Circular Arc |
- |
|
Parabolic Arc |
Parabolic arch defined with 3 nodes |
Start point, Intermediate point, End point N6;N7;N8 |
Parabolic Arc |
- |
|
Bezier |
Cubic Bezier curve |
Start point, 2nd point of control polygon (vertex), 3rd point of control polygon (vertex), End point N9;Vertex_B1_1; Vertex_B1_2;N10 |
Bezier |
N9 and N10 stands for start and end node Vertex_B1_1, Vertex_B1_2 define vertexes of bezier curve All values refers to list StrucutralPointConnection Bezier curve is parabolic, when 2nd and 3rd control points are the identical (values of coordinates are the same) |
|
Spline |
Curved line defined by polynomial function |
Start point, Set of mid points, End point N11;N12;N13;N14; N15;N16;N17;N18 |
Spline-8 |
“Spline-#” where “#” stands for number of nodes defining the spline |
|
Circle |
Circle |
Center Point, Point on the perimeter N36;N37 Or Three point on perimeter N36;N37;N38 |
Circle and Point or Circle by 3 points |
Circle is not valid to define StrucutralCurveMember |
|
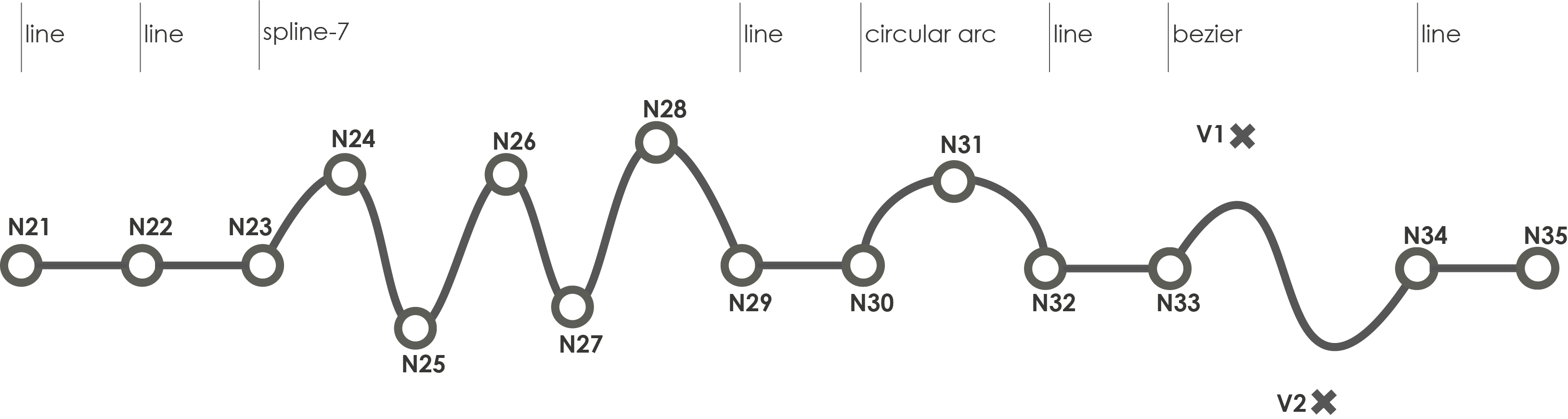
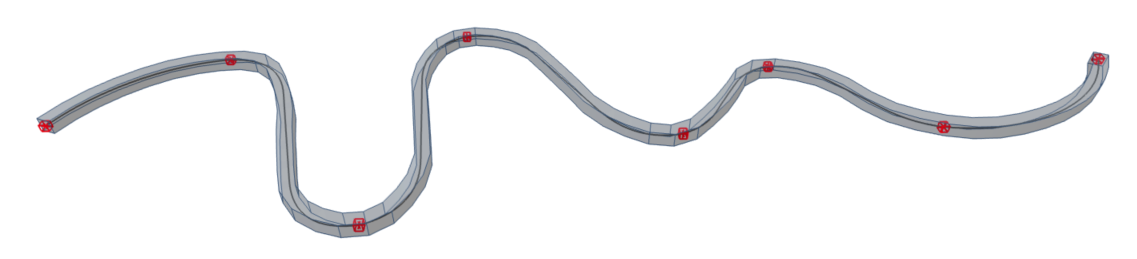
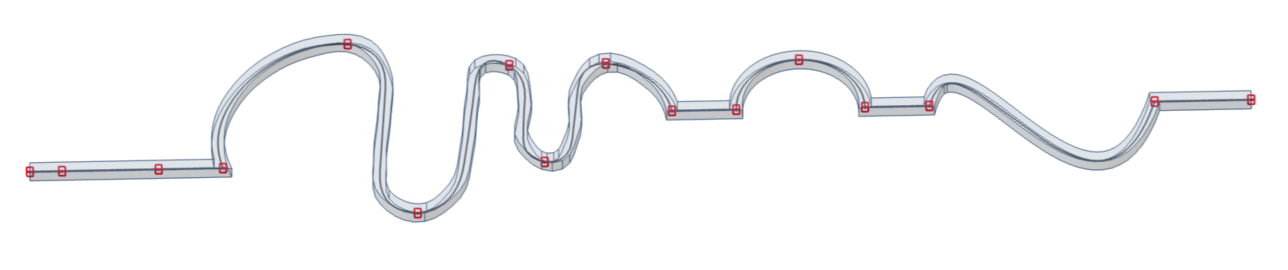
Polyline |
Combination of in nodes connected geometric types |
List of nodes N21;N22;N23;N24;N25; N26;N27;N28;N29;N30; N31;N32;N33;Vertex_B1_1; VertexB_1_2;N34;N35 |
Line;Line;Spline-7;Line;Circular Arc;Line;Bezier;Line |
Detail explanation can be found in notes below |
Notes¶
Mathematical definitions:
Bezier
\(Q(t)=\sum_{i=0}^{3}P_iB_i(t)\) ; \(t\epsilon<0,1>\)
\(B_{0t}=(1-t)^3,B_{1t}=3t(1-t)^2,B_{2t}=3t^2(1-t),B_{3t}=t^3\)
\(Q(t)\) is for the Bezier curve
\(P_{i}\) is for coodinates, and
\(B_{it}\) is for basis function
Spline
\(Q(t)=\sum_{i=0}^{m}P_iN_i^n(t)\) ; \(t\epsilon<t_i,t_{i+1}>\)
\(N_i^0(t)=1\) for \(t\epsilon<t_i,t_{i+1}>\)
\(N_i^0(t)=0\) otherwise
\(N{i}^{k}{(t)}=\frac{t-t_i}{t_{i+k}-t_i}N_{i}^{k-1}{(t)}+\frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}}N_{i+1}^{k-1}{(t)}\)
\(Q(t)\) is for the Spline curve
\(P_i\) is for the coordinates
\(N_i^n(t)\) is for basis function
\(n\) is for the degree of curve
\(m\) is for points of the control polygonPolyline schematics: